Modules libres sur un “monoïde”

Pendant des rappels d’algèbre commutative, un prof nous a rappelé la construction suivante : on part d’un anneau (commutatif, unitaire par simplicité – ce sera le cas de tou.te.s mes anneaux et algèbres dans ce post sauf mention expresse du contraire) $A$ , d’une $A$ -algèbre $B$ et d’un $A$ -module $M$ . On construit alors le produit tensoriel $B\otimes_A M$ , et on voit qu’on peut le munir d’une structure de $B$ -module, qui vérifie la propriété universelle suivante :

Proposition : Soit $N$ un $B$ -module, et $_AN$ le $A$ -module obtenu par restriction des scalaires. Alors $\hom_A(M, _AN) \to \hom_B(B\otimes_A M, N)$ défini par $f \mapsto (b\otimes_A m\mapsto bf(m) )$ est un isomorphisme, qui de plus est naturel en $M,N$ (et $B,A$ si on parvient à exprimer cette condition)

On peut éventuellement être surpris par un tel résultat la première fois qu’on le voit (après tout $\otimes_A$ est une opération qui peut être assez mystérieuse, surtout quand on l’a encore peu rencontrée), pourtant quand on le décortique on observe qu’il est complètement formel. C’est ce que je vais essayer de décrire dans ce qui suit.

Il y a deux notions importantes dans cette affaire : celle de catégorie monoïdale et celle de monoïde dans une telle catégorie. Je ne vais pas pouvoir m’attarder sur la première (ça mettrait trop de temps) et je vais donc seulement donner une idée assez précise pour nos objectifs de ce dont il s’agit :

Esquisse de définition : Soit $C$ une catégorie munie d’un bifoncteur $\otimes : C\times C\to C$ et d’un objet $I$ tel que :

On ait un isomorphisme (naturel en $A$ ) : $A\otimes I \cong A \cong I\otimes A$
On ait un isomorphisme $A\otimes (B\otimes C) \cong (A\otimes B)\otimes C$ (naturel en $A,B,C$ )

et on demande que ces isomorphismes naturels se comportent assez bien pour qu’on n’ait pas de souci en faisant les identifications qu’ils suggèrent (c’est cette partie là que je ne précise pas). On appelle alors la donnée de $C, \otimes, I$ (et, pour être précis, des isomorphismes naturels mentionnés) une catégorie monoïdale.

Exemples : Il y a tout un tas d’exemples qui permettront de mieux comprendre ce que j’entends par ma dernière phrase peu précise :

On prend $C = \mathbf{Set}$ la catégorie des ensembles, avec comme $\otimes$ le produit cartésien d’ensembles. Dans ce cas $I= \{*\}$ et on sait bien qu’on fait rarement attention à la distinction entre $A\times (B\times C)$ et $(A\times B)\times C$
On prend à nouveau $C= \mathbf{Set}$ mais cette fois-ci $\otimes$ l’union disjointe d’ensembles. Dans ce cas $I= \emptyset$ convient; et à nouveau on fait rarement la différence entre $A\sqcup (B\sqcup C)$ et $(A\sqcup B)\sqcup C$
Les deux exemples précédents se généralisent à n’importe quelle catégorie $C$ qui admet des produits (ou dualement, des coproduits) finis : $\otimes$ est le produit cartésien, $I$ l’objet terminal, et la condition d’associativité et d’unité se montrent de manière usuelle.
Soit $R$ un anneau non nécessairement commutatif, et $C$ la catégorie des $(R,R)$ -bimodules. Alors le produit tensoriel $\otimes_R$ fournit une structure de catégorie monoïdale. Plus simplement, si $A$ est un anneau, la catégorie des $A$ -modules a un produit tensoriel bien défini auquel on est plus habitué.
Si $M$ est un monoïde ordonné (c’est-à-dire un monoïde muni d’un ordre $\leq$ tel que $x\leq y \implies (xz\leq yz\land zx\leq zy)$ ) alors l’ordre sous-jacent, vu comme une catégorie, peut-être muni d’une structure de catégorie monoïdale où $\otimes$ est la multiplication de $M$ et $I$ le neutre de $M$ . Ici l’associativité est alors “on the nose” (i.e. pas à isomorphisme près) donc se comporte forcément bien.

Pour ne pas s’inquiéter de la dernière phrase de la définition : un célèbre théorème de MacLane annonce que toute catégorie monoïdale est monoïdalement équivalente (= équivalente en préservant toute la structure monoïdale à isomorphisme près) à une catégorie monoïdale stricte, c’est-à-dire où $A\otimes (B\otimes C) = (A\otimes B)\otimes C$ et $A\otimes I = A = I\otimes A$ (avec des vrais $=$ ), donc on peut toujours faire semblant qu’on a une telle catégorie. Voir cet article si on veut plus de précisions sur la définition de catégorie monoïdale.

À noter que dans une catégorie monoïdale en général, $\otimes$ peut être plus ou moins aussi bizarre qu’on le veut, donc potentiellement beaucoup plus bizarre que le produit tensoriel de $A$ -modules.

Maintenant, une définition importante :

Définition : Soit $(C,\otimes, I)$ une catégorie monoïdale. Soit $R$ un objet de $latexC$ muni de flèches $\mu : R\otimes R\to R$ et $\eta : I\to R$ . Le triplet $(R,\mu, \eta)$ est un monoïde dans $C$ si les diagrammes suivants commutent :

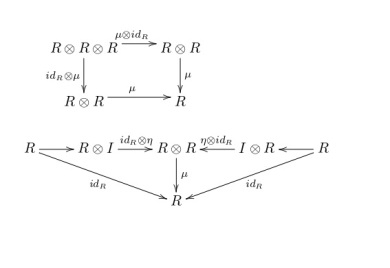
diagrammes_page-0001

Le premier symbolise l’associativité de $\mu$ , le second le fait que $\eta$ “choisit un élément neutre” de $R$ (les flèches $R\to R\otimes I$ et $R\to I\otimes R$ sont les isomorphismes canoniques donnés par la structure monoïdale)

Exemples : On reprend les catégories monoïdales données plus haut et on explicite ce qu’y est un monoïde:

Dans $\mathbf{Set}$ muni du produit cartésien, on observe facilement qu’un monoïde est précisément un monoïde au sens usuel du terme : un ensemble muni d’une multiplication associative et d’un neutre.
Dans $\mathbf{Set}$ muni de l’union disjointe (en fait dans n’importe quelle catégorie munie d’un coproduit et d’un objet initial comme structure monoïdale), on se rend compte facilement que les monoïdes sont exactement les objets, où le neutre est donné par l’unique flèche $\emptyset \to X$ et la multiplication par l’identité sur chaque composante $X\sqcup X \to X$ .
Si $A$ est un anneau, un monoïde dans la catégorie monoïdale des $A$ -modules munie du produit tensoriel est précisément une $A$ -algèbre non nécessairement commutative.
Dans un monoïde ordonné, un monoïde est précisément un élément $x$ plus grand que $1$ tel que $x^2 = x$ .

Dans le cas de $\mathbf{Set}$ muni du produit cartésien ou de $A-\mathbf{Mod}$ muni du produit tensoriel, on retrouve des objets auxquels on est habitué. On sait de plus que quand on a affaire à un monoïde ou à une algèbre, on a intérêt à regarder des modules dessus. C’est là qu’on va retomber sur nos pattes : on va définir dans une catégorie monoïdale quelconque ce qu’est un module sur un monoïde, et on va voir que le résultat énoncé au début de ce post est valable quelle que soit la catégorie monoïdale et quel que soit le monoïde: $R\otimes X$ sera toujours le $R$ -module libre sur $X$ .

Cela nous permettra en particulier de nous rappeler que $M\times X$ est l’action de $M$ libre sur $X$ lorsque $M$ est un monoïde (au sens usuel).

Pour définir un module, on mimique la définition de $A$ -module pour un anneau $A$ :

Définition : Soit $(C, \otimes, I)$ une catégorie monoïdale, $(R, \mu, \eta)$ un monoïde dans $C$ . Un $R$ -module (à gauche) est un objet $M$ de $C$ muni d’une flèche $\rho : R\otimes M \to M$ telle que les diagrammes suivants commutent :

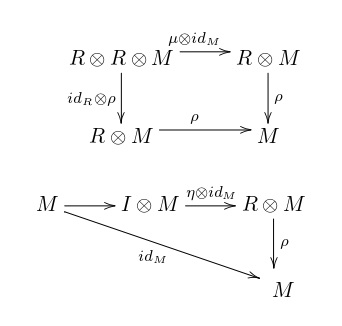
diagrammes (1)_page-0001

Ces diagrammes représentent les axiomes habituels de module : $(ab)m = a(bm)$ et $1m = m$ .

Exemples :

Dans $\mathbf{Set}$ munie du produit cartésien, un monoïde est un monoïde au sens usuel, et un $R$ -module est alors simplement un ensemble muni d’une action de $R$ , au sens usuel.
Un exemple peu intéressant, mais dans $\mathbf{Set}$ munie de l’union disjointe, on se rappelle qu’un monoïde est juste un ensemble, et alors un module $M$ sur cet ensemble $R$ n’est qu’une application $R\to M$ .
Si $A$ est un anneau, un monoïde dans la catégorie $A-\mathbf{Mod}$ muni du produit tensoriel usuel est une $A$ -algèbre $R$ non nécessairement commutative, et un $R$ -module est un $R$ -module à gauche au sens usuel.
Si $M$ est un monoïde ordonné, un monoïde est un objet $x$ avec $1\leq x = x^2$ et un $x$ -module est alors un objet $m$ tel que $xm \leq m$ donc tel que $xm = m$ (car $m = 1 m \leq xm$ )

Il est alors facile de définir la notion naturelle de morphisme de $R$ -modules, et de vérifier qu’on obtient ainsi une catégorie des $R$ -modules, qu’on notera $R-\mathbf{Mod}$ . Elle est munie d’un foncteur d’oubli $U$ vers $C$ (qui ne retient que $M$ et oublie la flèche $M\otimes R \to M$ ). La propriété qu’on veut obtenir est alors :

Proposition : $U$ a un adjoint à gauche, qui est défini sur les objets par $F : X \mapsto (R\otimes X, R\otimes R\otimes X \to X)$ , la flèche $R\otimes R\otimes X \to R\otimes X$ étant $\mu \otimes id_X$ .

La preuve n’est pas plus compliquée que l’énoncé. Il faut d’abord voir que $F$ peut être défini sur les flèches par $(X\overset{f}\to Y) \mapsto (R\otimes X \overset{id_R\otimes f}\to R\otimes Y)$ .

Une fois ça en main on observe que si $M$ est un $R$ -module et $X$ un objet de $C$ , on a une application composée $\varphi : \hom_C(X, M) \to \hom_C(R\otimes X, R\otimes M) \to \hom_C(X\otimes R, M)$ : la première application est $f\mapsto id_R\otimes f$ et la seconde est la postcomposition de $g: R\otimes X \to R\otimes M$ avec $\rho : R\otimes M\to M$ .

Le diagramme suivant montre que si $f: X\to M$ est une flèche, alors $\varphi(f) : R\otimes X \to M$ est un morphisme de $R$ -modules :

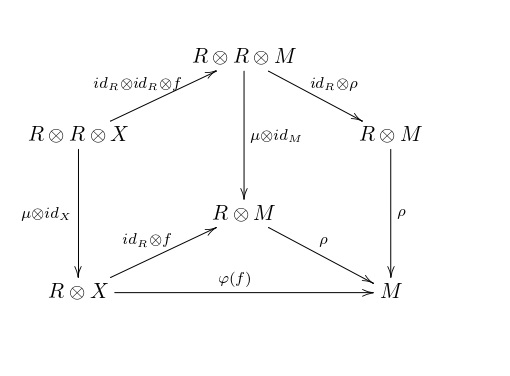
diagrammes (2)_page-0001

Où : le triangle du bas commute par définition de $\varphi(f)$ , le carré de droite commute parce que $M$ est un $R$ -module, le carré de gauche commute parce que $\otimes$ est un bifoncteur (et donc les deux chemins s’évaluent à $\mu\otimes f$ ); et la composée du haut $R\otimes R\otimes X\to R\otimes R\otimes M\to R\otimes M$ est par définition (et bifonctorialité de $\otimes$ ) $id_R\otimes \varphi(f)$ . Pour conclure il suffit alors d’enlever la flèche du milieu et de remplacer le triangle d’en haut par sa composée.

On corestreint alors $\varphi$ à l’ensemble des morphismes de $R$ -modules, et pour simplifier on lui garde la même notation.

Inversement, si on a un morphisme de $R$ -modules $f : R\otimes X \to M$ , alors on peut le précomposer avec $X \overset{\cong}\to I\otimes X \overset{\eta\otimes id_X}\to R\otimes X$ pour obtenir $\psi (f) : X \to M$ .

Les diagrammes suivants montrent que $\varphi, \psi$ sont inverses l’une de l’autre :

Dans le premier on part de $f:X\to M$ :

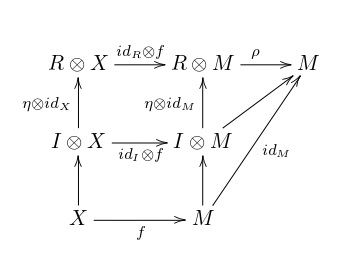
diagrammes (3)_page-0001

A ce stade, la commutation de chaque diagramme interne devrait être claire. En regardant les composées du $X$ en bas à gauche vers le $M$ en haut à droite, et en se rappelant les définitions, on voit que $\psi(\varphi(f)) = f$ .

Dans le second diagramme on part d’un morphisme de $R$ -modules $g : R\otimes X\to M$ :

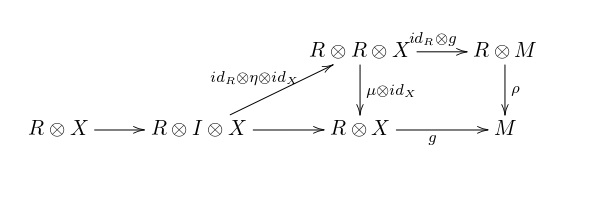
diagrammes (4)_page-0001

A nouveau il devrait être clair que le diagramme commute et si on regarde la composition du $R\otimes X$ le plus à gauche vers $M$ , en passant en bas on reconnait $g$ et en passant en haut on reconnait $\varphi(\psi(g))$ .

Il en découle que $\hom_C(X,UM) \cong \hom_{R-\mathbf{Mod}}(FX, M)$ . Une vérification que je ne ferai mais qui est évidente est que cette bijection est naturelle en $X,M$ . On a donc fini la preuve.

En particulier, quand on l’applique à nos exemples, on retrouve le résultat cité au tout début du post; et on retrouve aussi que $X\mapsto M\times X$ est le foncteur “ $M$ -action libre” lorsque $M$ est un monoïde au sens usuel.

Donc finalement, cette affaire avait très peu à faire avec le produit tensoriel usuel sur (disons) les groupes abéliens, mais est plutôt en lien avec l’idée même de produit tensoriel.

Pour conclure, j’irai plus loin dans le caractère formel de ce résultat en notant que, par le lemme de Yoneda, on peut transférer ce résultat à un cadre de catégories enrichies. En particulier, dans ce cadre et avec des hypothèses véritablement raisonnables on peut obtenir une adjonction enrichie au lieu d’une “simple” adjonction, ce qui ne fait qu’argumenter en faveur de la “formalité” de ce résultat. Pour plus d’informations, on pourra voir par exemple cette question et mon esquisse de réponse. Mais pour cette fois, je m’arrête ici.

Share this:

Related

Leave a comment Cancel reply